An online study guide for Regis High School by Zachary Espiritu.
Welcome to the Physics Mid-Year Study Guide 2016! If you're studying this guide, you probably have some vague desire of some kind to not fail Physics this trimester, so give yourself a pat on the back for taking the first step. This guide is structured in 6 acts:
Depending on how far back you are on your studying, you may wish to skim or even skip certain sections in the interest of time. If you're doing this, ideally you already know what you know and what you don't know so you can study what you don't know so you know it by the time you take the test (and if you don't know, it's probably circular motion). I've included some recommended study plans in this section which give you the best tips depending on how much time you have left to study, whether it's one week or a single all-nighter the day of the exam.
A few random tidbits: For easy navigation, I've included some anchor links (remember those from Computer Science?) in the sidebar to the left as you scroll to easily jump back and forth between sections. Also, if you're the type of person who likes to see things on a piece of paper, I've programmed this website such that it will automatically come out in a print-friendly format simply by printing normally from your browser.
Good luck on your studying escapades!
Just like the AP exam and the broken arm I had in the fifth grade, the Physics Midyear will be split in two parts.
You will have to answer 20 multiple choice questions on the test, each one worth 2 points each. These questions each have 4 answer choices from which you will have to choose the correct answer. (You could choose the incorrect answer, but I don't think that will help you in the long run.)
If you do the math, you'll realize that Part A is worth 40 points total.
You wil have to complete 6 free-response, multi-part questions on the test, each one worth 10 points each. Since the Physics gods are somewhat merciful, you'll have the opportunity to choose 6 questions out of 10 questions on the test. However, note that the Physics gods are still evil at heart, so you'll notice much, much, much overlap between the available questions on the test, so don't plan on skipping one problem type entirely.
Part B is worth 60 points total.
Depending on how much time you have, the suggested study plans below can help you get the most out of the little time you have:
In this system of just me and you, where I've defined negative to refer to the downwards direction, my acceleration is currently –9.8 m/s for you.
Chapter 2 contains material covering kinematics material in a single dimension. You'll be working on number lines for the majority of this chapter.
I'm assuming by this point you all know the standard kinematics equations for constant acceleration:
You'll be using these a lot.
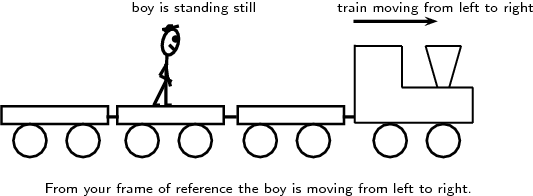
All of physics is measured relative to something else. The conceptual idea of reference frames is best explained by the image here: from your frame of reference on the ground, the boy is moving from left to right; from the boy's frame of reference, he is standing still.
Before doing any measurements in physics, we must define our reference frame. For most problems, this means you must define:
This will become especially important when dealing with vectors.
Displacement is defined as the change in position of an object. In other words, how far the object is from the starting point.
Displacement is a vector quantity, so make sure to include both magnitude and direction in your answer.
A person walks 70 meters west and 30 meters east. What is their displacement?
Speed is the measure of how fast an object is moving. The average speed of an object is defined as:
On the other hand, velocity is the measure of how fast and in what direction an object is moving (it's a vector quantity!). The numerical value of "how fast" is also known as the magnitude. Average velocity is defined as the displacement of an object over the time elapsed:
It's important to note that average speed uses total distance in its measurement as opposed to velocity, which uses displacement in its calculation. As a result, average speed and average velocity can be different for the same system.
Jack Ellwood runs 2 complete laps around a 400m circular track in 2.5 minutes. Determine the following:
Acceleration specifies how rapidly the velocity of an object is changing. Average acceleration is defined as the change in velocity divided by the time taken to make this change:
Acceleration is a vector quantity. Make sure to include the proper signage based on your chosen coordinate system.
A car accelerates along a straight road from rest to 75 km/h in 5.0 seconds. What is the magnitude of the average acceleration?
An important constant to memorize is the acceleration due to gravity on Earth, defined by \(g = 9.80\ m/s^2\).
A ball is thrown downward with an inital velocity of 3.00 m/s from a tower 70.0 meters high. Starting from the moment when the ball leaves the thrower's hand, how much time will have elapsed before the ball hits the ground?
We'll choose the \(y\) direction as negative downward, with the point at which the ball leaves the thrower's hand as \(y_0 = 0\).
We know that the vertical acceleration of the ball is \(a_y = -g = -9.8\). We also know that \(y_0 = 0\) and \(y = -70.0\ \mathrm{m}\), and we know that the initial vertical velocity is \(v_{0} = 3.00\ \mathrm{m/s}\).
We can now start solving for \(t\):
We can now use the quadratic equation to solve for \(t\).
Since a negative time is not possible, we know that the answer must be 4.098 seconds.
A ball is thrown upward into the air with an initial velocity of 15.0 m/s. Determine the following:
It's hard to draw graphs for this online, so you may wish to refer back to Lab 1 and Lab 2 for some good graphical drawing questions. Other than that, there's a few important points to note here:
A space probe accelerates uniformly from 50 m/s at \(t = 0\) to 150 m/s at \(t = 10\ \mathrm{s}\). How far did it move between \(t = 2.0\ \mathrm{s}\) and \(t = 6.0\ \mathrm{s}\)?
Chapter 3, quite unsuprisingly, is all about kinematics in two dimensions. Vectors become increasingly important here, as we'll see in a moment.
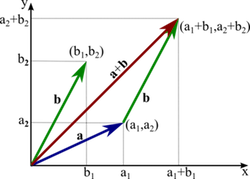
Remember that vectors have both magnitude and direction. As such, math with vectors needs to be handled in a special way.
We can add two vectors together by separating them into their horizontal and vertical components and adding those together separately. Afterwards, we can use the Pythagorean Theorem to determine the magnitude of the resultant vector and trignometry to determine the angular direction.
Similarly, we can subtract vectors in the same way.
We can also muliply a vector by a scalar. The direction will remain the same but the magnitude will equal the magnitude of the inital vector multiplied by the scalar. Make sure to remember to include direction in your answer.
An airplane trip involves three legs, with two stopovers for refueling. The first leg is due east for 620 km; the second leg is 45° south of east for 440 km; and the third leg is 50° south of west for 550 km. What is the plane's total displacement?
The projectile motion of an object can be understood by analyzing the horizontal and vertical components of an object separately.
A movie stunt driver on a motorcycle speeds horizontally off a 50.0 meter cliff. How fast must the motorcycle leave the cliff to land 90.0 meters from the base of the cliff?
We'll choose the \(y\) direction as positive upward, with the top of the cliff as \(y_0 = 0\). The \(x\) direction is horizontal with \(x_0 = 0\) at the point where the motorcycle leaves the cliff.
We know that the vertical acceleration of the motorcycle is \(a_y = -g = -9.8\) and that the horizontal acceleration of the motorcycle is \(a_x = 0\). We also know that \(y_0 = 0\) and \(y = -50.0\ \mathrm{m}\), and that \(x_0 = 0\) and \(x = 90.0\ \mathrm{m}\). Finally, we know that the initial vertical velocity is \(v_{y0} = 0\).
We can now start by setting up our equation for solving \(t\):
We can then solve for \(t\) and set \(y = 50.0\ \mathrm{m}\).
Now, we can calculate for the initial velocity, \(v_{x0}\).
The motorcycle must leave the cliff at a speed of 28.2 m/s.
A football is kicked at an angle \({\theta}_0 = 37.0°\) with a velocity of 20.0 m/s. Determine the following:
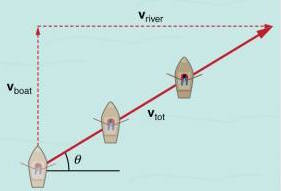
Relative velocity is where the concept of reference frames from Chapter 2 becomes especially important. At the end of the day, however, problems dealing with relative velocity essentially are more addition of vectors.
The picture here best demonstrates this concept. A boat trying to head straight across a flowing river will actually move diagonally relative to the shore as shown. The boat's velocity (solid arrow) relative to the shore is the sum of its forward velocity relative to the river plus the horizontal velocity of the river relative to the shore.
One of the more common problem types for relative velocity are moving boat problems. The main thing to remember here is that in order to travel directly across a river, a boat must point itself at an upstream angle in order to counteract the movement of the flowing river. If the boat positions itself pointing straight across the river, it will end up in a position more downstream due to the current of the river.
A boat with a speed of \(v_{\mathrm{boat}} = 1.85\ \mathrm{m/s}\) is travelling in a river with a current of speed \(v_{\mathrm{current}} = 1.20\ \mathrm{m/s}\). If the boat wants to travel directly across the river, at what upstream angle must the boat head?
Two kittens are on a roof. Which one falls off first?
The one with the lowest mu.
Cat physics jokes aside, Chapter 4 is all about the relationship between force and motion.
As we all should know by now, a force is any type of push or pull on a object. They are vector quantities, so they have both magnitude and direction. The important (and slightly unintunitive) thing to remember about forces is that an object will continue to remain at rest or move at constant speed if no force is being applied to it. In other words, an object only will slow down or speed up if a force is applied on it.
Newton's three laws of motion describe the behavior of objects when forces are applied to them. For the test, expect some of the multiple choice questions in Part 1 to use concepts from Newton's First and Third Law of Motion, and to use Newton's Second Law of Motion in Part 2.
Every object continues in its state of rest, or of uniform velocity in a straight line, as long as no net force acts on it.
As we all should know by now, a force is any type of push or pull on a object. Newton's first law of motion describes an important (and slightly unintunitive) thing to remember about forces is that an object will continue to remain at rest or move at constant speed if no force is being applied to it. In other words, an object only will slow down or speed up if a force is applied on it.
This tendency of an object to maintain its state of rest or uniform motion is called inertia.
The acceleration of an object is directly proportional to the net force acting on it, and is inversely proportional to its mass. The direction of the acceleration is in the direction of the net force action on the object.
Newton's second law of motion is best known in its equation form:
Remember before solving to convert your mass units to kilograms to stay in line with SI units.
What average net force is required to bring a 1500-kg car to rest from a speed of 28 m/s within a distance of 55 meters?
We'll define the car's motion as along the positive x-axis. We know that that the initial velocity \(v_0 = 28\ \mathrm{m/s}\), the final velocity \(v = 0\), and the distance \(\Delta{x} = 55\ \mathrm{m}\).
In order to determine the force, we still need to find \(a\), so let's set up a kinematic equation:
Now, we can plug our values into \(F = ma\) and solve for \(F\):
The force required to stop the car is \(-1.1 \times 10^4\ \mathrm{N}\). Note that the force must be exerted in the direction opposite to the initial velocity, which the negative symbol signifies.
Whenever one object exerts a force on a second object, the second exerts an equal force in the opposite direction on the first.
Newton's third law of motion is more commonly known as "to every action there is an equal and opposite reaction". The important thing to note here is that the "action" force and the "reaction" force are acting on different objects.
A good example of Newton's third law in action are cars. The tires of a moving car push backward against the ground because of friction, and the ground pushes on the tires in the opposite direction, accelerating the car forward.
Mass is best defined as the measure of the inertia of an object. The more mass an object has, the greater the force needed to give it a particular acceleration.
The SI unit for mass is the kilogram (kg).
Weight, on the other hand, is defined as the magnitude of the gravitational force on an object. The gravitational force on an object can be written as \(\vec{F}_G = m\vec{g}\).
A woman weighing 65 kilograms descends in a elevator that briefly accelerates at \(0.20g\) downard when leaving a floor. She stands on a scale that reads in kilograms.
Part A: From Newton's Second Law of Motion, we know:
We can now solve for \(F_\mathrm{N}\):
The normal force \(\vec{F}_\mathrm{N}\) is the force the scale exerts on the person. While her weight (the force of gravity on her) will always be \(mg = (65\ \mathrm{kg})(9.8\ \mathrm{m/s^2}) = 640\ \mathrm{N}\), the scale only needs to exert a force of \(0.80mg\), so it will give a reading of \(0.80m = \mathbf{52\ kg}.\)
Part B: Since there is no acceleration, by Newton's Second Law of Motion, we know that \(mg - F_\mathrm{N} = 0\), so \(mg = F_\mathrm{N}\). The scale reads her true mass of 65 kilograms.
A student whose weight is 600 newtons is standing in an elevator. If the elevator rises with an acceleration of 9.8 m/s2, what is the force the elevator exerts on the student?
The final concept to remember in this section is normal force, written as \(\vec{F}_N\), which is defined as a contact force that acts perpendicular to the surface of contact. An example of a normal force is the force exerted by a table on a box placed on top of it. Using Newton's Third Law of Motion, we know that \(\vec{F}_N = \vec{F}_G\) of the box.
In some cases, however, the normal force isn't equal to \(\vec{F}_G\)—for the example above, this may be when the box in question is placed on an incline, or when an external force is pushing the box downwards.
A friend has given you a special gift, a box of mass 10.0 kilograms with a mystery surprise inside. (I'm not kidding, that's actually the wording for one of the problems in the textbook.) The box is resting on a frictionless, surface.
When solving problems involving Newton's laws and force, you should draw a free-body diagram that shows all of the forces acting on each object involved. You all should know how to draw one by now, so there's no need to include an example here, but remember: do not to include forces that the chosen object exerts on other objects; only forces that are exerted on the chosen object.
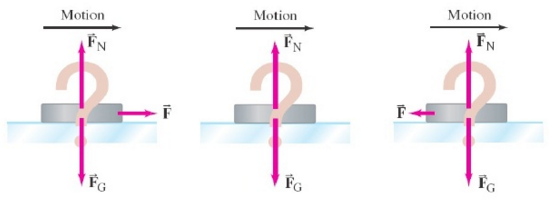
A hockey puck is sliding at constant velocity across a flat horizontal ice surface.
If the surface is assumed to be frictionless, which one of the free-body diagrams in the picture is the correct free-body diagram for this puck? What would the answer be if the puck slowed down?
A deer box weighing 10.0 kilograms is placed on a flat, frictionless surface. A cord is attached to the box, and Ankeith pulls the cord, moving the box across the table. The magnitude of the force exerted by the pull is \(F_P = 40.0\ \mathrm{N}\), and it is exerted at a 30.0° angle as shown. Determine the following:
Speaking of rope problems, another concept you'll need to remember is tension, which is the force, \(F_T\), that a cord exerts on an object.
Two boxes are connected by a lightweight cord and are resting on a frictionless table. The boxes have masses of 12.0 kilograms and 10.0 kilograms. A horizontal force, \(F_P\), of 40.0 N is applied to the 10.0 kilogram box. Determine the following:
There are two types of friction: kinetic friction and static friction.
Kinetic friction occurs when two objects slide against one another. It is proportional to the normal force exerted by the object:
Here, \(\mathbf{{\mu}_k}\) refers to the coefficient of kinetic friction, which can only be determined experimentally. As a result, many of the problems you will encounter will either provide the value of \(\mu\) for you or have you solve directly for \(\mu\).
Static friction refers to a force parallel to two surfaces in contact with each other when the two objects are not sliding. The equation used is similar to kinetic friction, albeit with a few changes:
Here, \(\mathbf{{\mu}_s}\) refers to the coefficient of static friction (not to be confused with \(\mathbf{{\mu}_k}\)). We use a \(\le\) sign here as the force of static friction can vary from zero to the maximum value given by \({\mu}_s F_N\).
This concept of changing static friction is best demonstrated by pushing on a heavy table. When you're not pushing on the table, the floor is not exerting any horizontal force on the table. However, if you begin to push horizontally on the table, and the table doesn't move, the floor has begun to exert the force of static friction against the table. Incresaing the force of pushing will also increase the force of static friction until it reaches its upper bound (given by the above equation), at which point the table will begin to move.
A 10 kilogram box rests on a horizontal floor. The coefficient of static friction is \({\mu}_s = 0.40\) and the coefficient of kinetic friction is \({\mu}_k = 0.30\). Determine the force of the friction, \(F_{fr}\), acting on the box if a horizontal external applied force \(F_A\) is exerted on it for the following magnitudes:
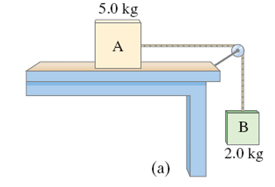
Two boxes, \(A\) (5.0 kilograms) and \(B\) (2.0 kilograms), shown in the figure here, are connected by a cord running over a pulley. Box \(A\) is placed on a flat, level table and box \(B\) is left hanging off the side of the table. The coefficient of kinetic friction between box \(A\) and the table is \(0.20\). Ignoring the mass of the cord and the pulley and any friction in the pulley, what is the acceleration \(a\) of the system?
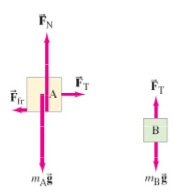
To solve this problem, we'll draw a free-body diagram for each of the boxes, as shown in the second figure. We also know that the horizontal accleration of box \(A\) must be equal to the vertical accleration of box \(B\). More on that later.
We know that box \(A\) doesn't move vertically, so Newton's second law tells us the normal force is equal to the weight:
In the horizontal direction, there are two forces on box \(A\): \(F_{\mathrm{T}}\), the tension in the cord (which we don't know yet), and the force of friction, \(F_{\mathrm{fr}}\). We'll start by solving for \(F_{\mathrm{fr}}\):
We want to solve for the horizontal acceleration of box A, so let's set up a force equation that will let us do that:
Now, let's consider box B. Let's solve for \(m_{\mathrm{B}}g\):
Since we want to solve for the vertical accleration of box \(B\), let's setup our force equation:
Using our box \(A\) equation from earlier, we can solve for \(F_{\mathrm{T}}\) and substitute into our box \(B\) equation:
We can now solve for \(a\) and plug in our values:
The acceleration of the two boxes is 1.4 m/s2, with box \(A\) accelerating towards the right and box \(B\) acclerating towards the ground.
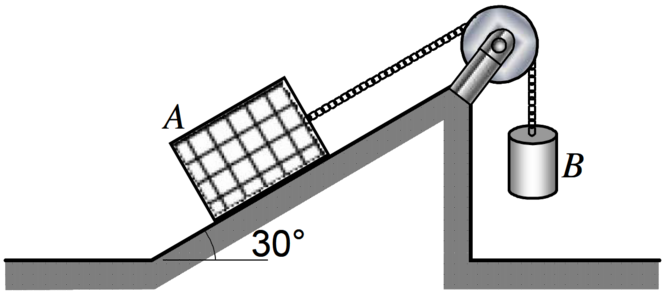
Two boxes, \(A\) and \(B\), shown in the figure here, are connected by a cord running over a pulley. Box \(A\) weighs 100 kilograms and placed on a ramp inclined at 30°. The coefficient of static friction between box \(A\) and the ramp is 0.30. Determine the minimum weight of box \(B\) require to prevent box \(A\) from sliding down on the ramp.
Chapter 5 is all about circular motion and gravitation, and then doing the terrible thing of combining both of them into satellite problems to make people sad.
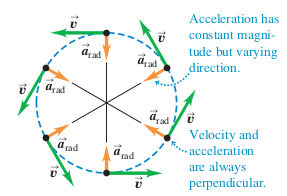
An object that moves in a circle at constant speed \(v\) is said to experience uniform circular motion. The magnitude of the velocity remains constant throughout the object's motion, but the direction of the velocity is constantly changing.
Because acceleration is defined as a change of velocity, an object undergoing uniform circular motion is constantly changing velocity.
We can calculate the acceleration of an object undergoing uniform circular motion as follows:
The accleration vector always points towards the center of the circle.
We can also create an equation to determine the velocity of an object undergoing uniform circular motion:
Assume the Moon has a uniform circular orbit around the Earth of radius 384,000 kilometers with a period \(T\) of 27.3 days. Determine the acceleration of the Moon toward the Earth.
You may encounter problems that deal with force and uniform circular motion together. For example, an object moving in a circle, such as a ball on the end of a string, must have a force applied to it to keep it moving in that circle. The magnitude of this force can be calculated using Newton's second law and the uniform circular motion accleration above:
Calculate the force a person must exert on a string attached to a 0.150 kilogram ball to make the ball revolve in a horizontal circule of radius 0.600 meters. The ball makes 2.00 revolutions per second.
A 0.150 kilogram ball on the end of a 1.10-meter-long cord is swing in a vertical circle. Determine the following:
Newton's Law of Universal Gravitation states that, essentially, everything attracts everything else. The magnitude of the gravitational force between two objects of masses \(m_1\) and \(m_2\) can be written as:
\(G\) refers to the universal gravitation constant:
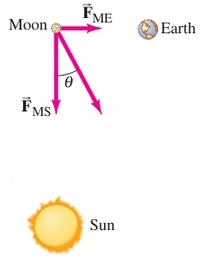
Find the net force on the Moon (\(m_M = 7.35 \times 10^{22}\ \mathrm{kg}\)) due to the gravitational attraction of both the Earth (\(m_E = 5.98 \times 10^{24}\ \mathrm{kg}\)) and the Sun (\(m_S = 1.99 \times 10^{30}\ \mathrm{kg}\)), assuming they are at right angles to each other.
Artifical satellies ciriculing the Earth are put into orbit by accelerating them to a sufficiently high tangential speed. If the speed is too high, they will escape orbit and fly off into space. If the speed is too low, they will fall back to Earth.
Note that satellites are in constant freefall to the Earth, which is why we can use the concepts of uniform circular motion and universal gravitation together to describe their motion.
A geosynchronous satellite is one that has a period of one day. Knowing that the mass of the Earth is \(m_E = 5.98 \times 10^{24}\ \mathrm{kg}\), determine the following:
Chapter 6 explores the concepts of work and energy, which further describe forces. They are scalar quantities, which makes them, quite thankfully, easier to work with than vectors.
The work done on an object by a constant force can be defined via the following equation:
where \(F\) is the magnitude of the constant force, \(d\) is the magnitude of the displacement of the object, and \(\theta\) is the angle between the directions of the force and the displacement. In simpler terms, \(F\cos{\theta}\) refers to the magnitude of the force parallel to \(d\).
Work is measured in joules (J).
Remember that a force can be exerted on an object yet do no work if there is no displacement.
A person pulls a 50 kilogram create 40 meters along a horizontal floor by a constant force \(F_\mathrm{P} = 100\ \mathrm{N}\), which acts at a 37° angle above the horizontal. The floor exerts a friction force on the box of \(F_\mathrm{fr} = 50\ \mathrm{N}\). Determine the following:
A potential question may be determining the work done by a varying force as described by a graph. The area under the curve is equal to the work done.
In its simplest terms, energy is defined as "the ability to do work". There are two types of energy: kinetic and potential.
Kinetic energy is the energy associated with an object in motion. It can be calculated via the following equation:
The work done by a force is equal to the change in kinetic energy:
How much net work is required to accelerate a 1000 kilogram car from 20 m/s to 30 m/s?
Potential energy is the energy associated with forces that depend on the position of an object relative to its surroundings. For the purposes of this test, you need to be familiar with two types of potential energy: gravitational potential energy, discussed below, and elastic potential energy, which will be discussed in the Springs section.
Gravitational potential energy can be calculated with the following equation:
To compress a spring some distance \(x\), a force \(F_\mathrm{P}\) must be applied that is directly proportional to \(x\):
Here, \(k\) refers to the spring stiffness constant, and is a measure of the stiffness of the particular spring. The problems you'll be encountering will usually give you what \(k\) is equal to upfront, but some may have you determine the value of \(k\) algebraically.
In addition, springs have elastic potential energy when compressed or stretched. It can be calculated with the following equation:
We all know about the Law of Conservation of Energy, which states that energy cannot be created or destroyed, only converted to another form. The majority of the forces you'll be encountering are conservative forces, which keep all the energy exerted inside of the system.
However, there also exists nonconservative forces, which release energy outside of the system. An example of this is friction—when a box is pushed against a rough surface, some of the energy is released into the surrounding area as heat energy.
Assuming we are only dealing with conservative forces, mechanical energy is defined as the sum of the kinetic and potential energies in a system at any given moment:
You'll usually use this concept to compare energy changes in a system at different points in time:
A rock is dropped from a height of \(h = 3.0\ \mathrm{m}\). Calculate the rock's speed when it has fallen to 1.0 meter above the ground.
While this problem seems like it doesn't have enough information, you actually have enough information to solve the problem using the mechanical energy concepts seen above. We know that at the moment of release, the rock's position is \(h_1 = 3.0\ \mathrm{m}\) and it's velocity is \(v_1 = 0\). We want to find \(v_2\) when the rock is at position (\y_2 = 2.0\ \mathrm{m}\). We can set up our conservation equation as such:
The \(m\)'s cancel out, allowing us to solve for \(v_2\):
We can then take the square root to get our answer.
The rock's speed will be 6.3 m/s2 when it reaches a height of 1.0 meter.
You might encounter a problem that asks you to deal with springs and conservation of energy at the same time:
A dart of mass 0.100 kilograms is pressed against the spring of a toy dart gun. The spring (\(k = 250\ \mathrm{N/m}\)) is compressed 6.0 centimeters and released. If the dart detaches from the spring when the spring reaches its natural length (\(x = 0\)), what speed does the dart acquire?